
Understanding Probability: A Beginner's Guide with a Probability Calculator
Probability is a fundamental concept in mathematics and statistics that plays a crucial role in our daily lives, from predicting weather patterns to making informed decisions in various fields like finance, science, and gaming. In this beginner's guide, we will delve into the world of probability, demystify its core principles, and introduce you to a handy online free probability calculator to make calculations easier.
What is Probability?
Probability is a measure of the likelihood or chance that a specific event will occur. It is expressed as a number between 0 and 1, where 0 indicates an event is impossible, and 1 denotes absolute certainty. Everything in between represents varying degrees of uncertainty.
To understand probability better, consider a simple example: flipping a fair coin. When you flip a coin, there are two possible outcomes: heads or tails. The probability of getting heads is 0.5, and the probability of getting tails is also 0.5. This means that there is an equal chance of getting either outcome.
Probability Basics
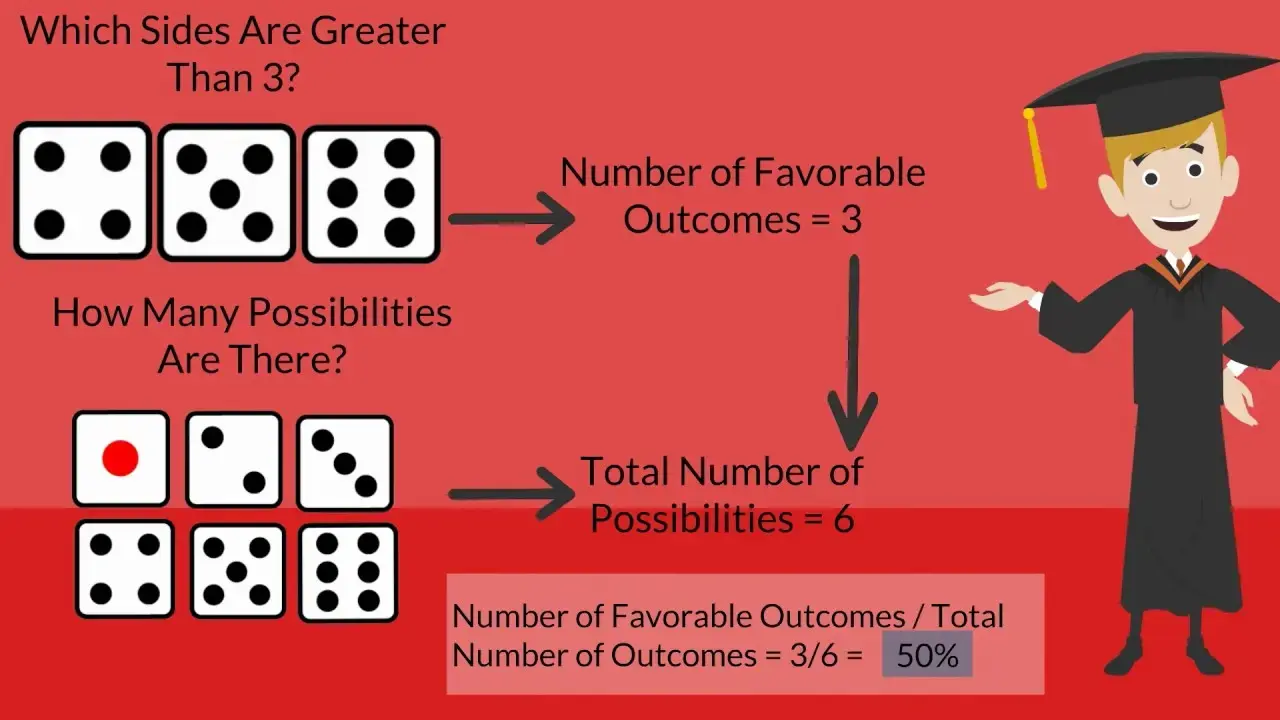
Before we explore more complex probability scenarios, let's cover some essential concepts:
- Sample Space: The sample space is the set of all possible outcomes of an experiment. For a fair six-sided die roll, the sample space is {1, 2, 3, 4, 5, 6}.
- Event: An event is a subset of the sample space. For example, if we are interested in the event "rolling an even number" with a six-sided die, the event would be {2, 4, 6}.
- Probability of an Event: The probability of an event is calculated by dividing the number of favorable outcomes (outcomes that meet the event's criteria) by the total number of possible outcomes in the sample space.
- Complementary Events: The probability of the complementary event (not the event of interest) is equal to 1 minus the probability of the event itself. For example, if the probability of rain is 0.3, the probability of no rain is 0.7.
Probability Calculator
To make probability calculations easier, you can use a probability calculator. These online tools allow you to input the relevant data and obtain probability values quickly. Let's walk through an example using a probability calculator:
Probability calculators are valuable tools for quickly obtaining probabilities in various scenarios, from card games to business decisions.
Look into more additional free tools: Top Website Screenshot Generator Tools: A Comparative Review
Types of Probability

Probability can be classified into several categories, each suited to different situations:
- Classical Probability: This type of probability applies to situations with equally likely outcomes, such as rolling a fair die or flipping a fair coin.
- Empirical Probability: Empirical probability is based on observed data. It involves collecting data from real-world experiments and calculating probabilities based on the frequency of events. For example, determining the probability of a car accident at a specific intersection based on historical accident data.
- Subjective Probability: Subjective probability is based on personal judgments or beliefs. It is often used when objective data is unavailable or unreliable. For instance, estimating the probability of a certain political candidate winning an election based on opinion polls.
- Conditional Probability: Conditional probability refers to the probability of an event occurring given that another event has already occurred.
Probability Rules
Several rules and theorems help us calculate probabilities in more complex scenarios:
- Multiplication Rule: The probability of two independent events both occurring is the product of their individual probabilities. Independent events are events that do not affect each other.
- Bayes' Theorem: Bayes' Theorem is used to update probabilities when new information becomes available. It is particularly useful in conditional probability problems and is commonly applied in fields like machine learning and statistics.
Applications of Probability

Probability has wide-ranging applications in various fields:
- Statistics: Probability is fundamental in statistical analysis, where it helps quantify uncertainty and make inferences about populations based on sample data.
- Finance: Probability is crucial in risk assessment, portfolio management, and pricing financial derivatives.
- Weather Forecasting: Meteorologists use probability models to predict weather patterns and the likelihood of specific weather events.
- Gaming and Gambling: Probability plays a significant role in casino games, lotteries, and sports betting, helping both players and operators make informed decisions.
- Medical Diagnosis: Doctors use probability to assess the likelihood of diseases based on symptoms and test results.
Free Tools: Free HTML Minifier Tool Online | Free URL Opener Tool Online
Conclusion
Probability is a powerful tool for understanding and quantifying uncertainty in various aspects of life. From predicting outcomes in games of chance to making data-driven decisions in finance and science, a solid grasp of probability is invaluable. With the help of probability calculators and a clear understanding of its principles, you can navigate the world of uncertainty with confidence and make informed choices. So, whether you're rolling dice, drawing cards, or analyzing data, probability is your guide to making sense of chance.
Click this link to get additional free tools: Simplify HTML Inspection with Online HTML Viewer Tools
Frequently Asked Questions
1. What is probability?
Probability is a measure of the likelihood or chance of an event occurring.
2. How is probability expressed?
Probability is expressed as a number between 0 and 1, where 0 means impossible and 1 means certain.
3. What is the difference between theoretical and experimental probability?
Theoretical probability is based on mathematical calculations, while experimental probability is determined through real-world experiments or observations.
4. What is the probability of rolling a fair six-sided die and getting a 3?
The probability is 1/6, as there is one favorable outcome (rolling a 3) out of six possible outcomes.
5. What is the complement of an event in probability?
The complement of an event is the probability of the event not happening. It is calculated as 1 minus the probability of the event occurring.
6. What is conditional probability?
Conditional probability is the probability of an event occurring given that another event has already occurred.
7. How do you calculate the probability of multiple independent events occurring together?
Multiply the individual probabilities of each event to find the probability of all events happening together.
8. What is the law of large numbers in probability?
The law of large numbers states that as the number of trials or experiments increases, the experimental probability will approach the theoretical probability.
9. How can I use a probability calculator?
A probability calculator helps you compute probabilities quickly. Input the relevant data, such as sample space and favorable outcomes, and the calculator will provide the probability result.



